La Trigonometría y la Astronomía
La
trigonometría fue motivada por el deseo de los antiguos astrónomos griegos de
tener herramientas para poder describir trayectorias o posiciones de los
cuerpos celestes, así como para saber la hora en un momento determinado,
especialmente en las noches, tener un calendario, herramientas para la
navegación y la geografía. Aunque la trigonometría de los antiguos griegos es
lo que hoy se conoce con el nombre de trigonometría esférica, lo esencial de la
trigonometría plana está íntimamente relacionado con ella.
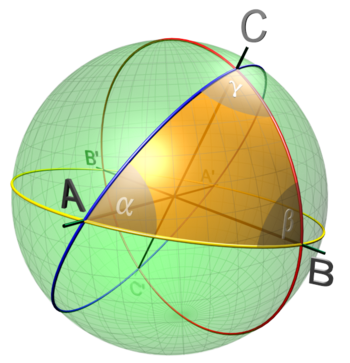
Ahora bien la
trigonometría esférica supone la geometría esférica. En esta se consideran los
círculos máximos, y los triángulos que se puedan construir con ellos. La
trigonometría permite relacionar medidas angulares con medidas lineales. Son
los pitagóricos los que le van a dar el carácter matemático a la astronomía.
Recordemos que para ellos todo es número o relaciones entre números y la
matemática estaba constituida por el quadrivium: aritmética y su
aplicación la música, geometría y su aplicación la astronomía.
Euclides en
su libro Fenómenos tiene algo de geometría esférica, con teoremas que
intentaban explicar los movimientos aparentes de las estrellas. Teodosio (20
a.C) recolectó, al estilo de Euclides en los Elementos, el conocimiento
disponible en su época sobre geometría esférica, pero su trabajo no permitía
tratar el problema fundamental de la astronomía, a saber: determinar la hora en
la noche observando las estrellas.
Se reconoce en Hiparco de Nicea (c. 125 a.C) al
fundador de la trigonometría.
Hiparco vivió
en Rodas y en Alejandría y debemos a él varios descubrimientos y observaciones
astronómicas; realizó la teoría astronómica más influyente de su época. Se conserva
sus Comentarios a los Fenómenos de Eudoxio y Aratus. Eudoxio fue uno de
los grandes matemáticos griegos, autor posiblemente de los resultados de libro
V de los Elementos y Aratus fue un respetado poeta griego, quien tiene
un libro llamado Fenómenos, en el cual se refiere a la astronomía.
El método de Hiparco de Nicea
El método, descrito por Tolomeo es el siguiente:
1. Dividió
la circunferencia en 360º.
2. Dividió
el diámetro de la circunferencia en 120 partes.
3. Cada
parte de la circunferencia y cada parte del diámetro las dividió a su vez en 60
partes, y cada una de estas en 60 partes nuevamente.
4. A
cada arco de circunferencia AB le hacía corresponder el número de unidades
tanto de la cuerda correspondiente como del radio respectivo. El número de
unidades de la cuerda corresponde a lo que hoy llamamos la función seno.
Si
2a es el ángulo central del arco AB, entonces para
nosotros sen a = AC/OA,
mientras para Hiparco sen a es el número
de unidades en 2AC cuando el radio contiene 60 unidades. Por ejemplo si la
cuerda de 2a es AB y
tiene 40 unidades, entonces sen a = 20/60. Lo cual en sus términos sería.
Menéalo y su Esférica
La trigonometría griega alcanza un gran
desarrollo con Menelao (c. 98 d.C) Su trabajo más importante se titula Esférica, y
aparentemente también escribió un tratado de seis libros titulado Cuerdas en
un círculo. Entre los objetivos del primer libro de la Esférica está
demostrar teoremas al estilo de los teoremas de los triángulos planos en la
obra de Euclides. Menelao, sin embargo, prueba un teorema característico de los
triángulos esféricos y que no vale en la geometría plana: si dos triángulos
tienen sus tres ángulos iguales los triángulos son iguales; en geometría plana
en ese caso los triángulos serían semejantes.
El Almagesto de Tolomeo
El desarrollo de la trigonometría griega y
su aplicación a la astronomía culmina con los trabajos de Tolomeo (100 -170).
La astronomía y la trigonometría están mezcladas en los trece libros del Almagesto. Este es un tratado matemático, excepto cuando
usa la física aristotélica para refutar el modelo heliocéntrico del universo
conocido para ellos que había propuesto Aristarco de Samos en el siglo IV a.C.
Tolomeo aplicó sus
estudios de trigonometría a la
construcción de astrolabios y relojes de sol. Y también aplicó el estudio de la
astronomía al de la astrología, creando los horóscopos. Todas estas teorías y
estudios están escritos en su obra Tetrabiblon.
La
trigonometría en el Renacimiento
Hasta
mediados del siglo XV la trigonometría estudiada y aplicada era esencialmente
la trigonometría esférica. En esta época la trigonometría plana se convierte en
una herramienta importante para la agrimensura, aunque Leonardo de Pisa, el mismo
Fibonacci (1180-1240) dos siglos atrás ya había comenzado a usarla con los
mismos propósitos. Los nuevos desarrollos en trigonometría se deben a los
alemanes, motivados como en la antigüedad por la navegación, la construcción de
calendarios y naturalmente la astronomía, debido a la reciente creación de la
teoría heliocéntrica de Copernico (1473-1543).
George
Peurbach (1423-1461) corrigió la versión árabe del Almagesto y comenzó a
realizar tablas trigonométricas más precisas. Pero Peurbach murió muy joven y
su alumno Johannes Müller (1436-1476), llamado Regio montano, estudió los
tratados más importantes de griegos, hindúes y sus contemporáneos; construyó la
tabla de los senos basado en un radio de 600.000 unidades y otra basada en un
radio de 10.000.000 unidades. Regio montano estableció la ley de los senos para
la geometría esférica y una ley de los cosenos. De Triangulis Omnimodis (Sobre triángulos de todo tipo) es el título de la obra
de Regio montano y está estructurada de una forma muy similar a los Elementos
de Euclides.
Regiomontano
. De
triangulis se compone de cinco libros, en el primero da las definiciones
básicas: cantidad, ratio, igualdad, círculos, arcos, cuerdas, y la función
seno. Proporciona algunos axiomas que proporcionarán el sustento de los 56
teoremas que enunciará. En el segundo de los libros establece la ley del
seno y la emplea en la resolución de algunos problemas con triángulos.
Determina el área de un triángulo mediante el conocimiento de dos lados y el
ángulo que los sustenta. Los libros III, IV y V tratan de trigonometría
fundamentando el tema para las posteriores obras de astronomía.
Bartolomeo
Pitiscus (1561-1613) usó por primera vez el nombre de trigonometría en
un trabajo de 1595 que se publicó como suplemento a un libro suyo sobre
“esférica”.
François Viète
Por último mencionaremos a François Viète
(1540-1603), abogado de profesión, reconocido como uno de los matemáticos más
importantes del siglo XVI. Entre 1564 y 1568,
se sumerge en trabajos de astronomía y trigonometría y redacta un tratado que
quedará inédito: Harmonicon Cœleste. En 1571, publica una obra de
trigonometría, el Canon mathematicus en el que presenta numerosas
fórmulas relacionadas con senos y cosenos. Emplea de modo poco habitual para la
época los números decimales.
En el siglo XVI la trigonometría comenzó a
independizarse de la astronomía y adquirió el estatus de una rama de las
matemáticas, a partir de la obra de Regio montano.
BIBLIOGRAFÍA.
•
Este recuento ha sido esencialmente elaborado
teniendo como fuente el libro de Morris Kline Mathematical Thougth from
Ancient to Modern Times, Oxford University Press, 1972.
•
De gran ayuda ha sido igualmente internet y
particularmente la wikipedia.
•
Agradezco a Yesid Puerto el siguiente enlace que
tendré en cuenta para una próxima versión mejorada y que recomiendo a los estudiantes
interesados en este tema:http://press.princeton.edu/books/maor/